各类积分的总结

各种积分之间的联系

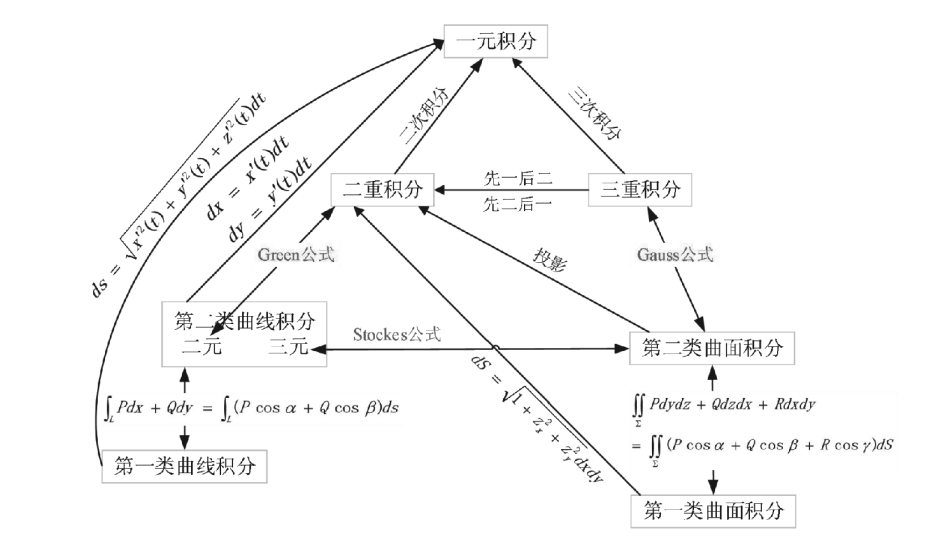
几何意义

一元积分就是函数到 x 坐标轴的面积；
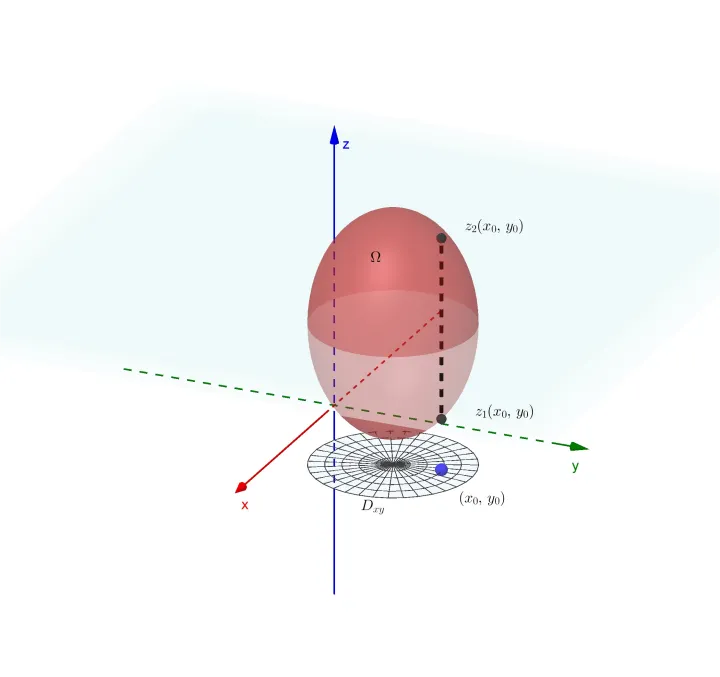
二重积分就是函数到 xy 坐标面的体积；
三重积分表示四维测度；
第一类曲线积分可以认为是准线为积分曲线，母线平行于 z 轴的柱面的面积；
第一类曲面积分表示体积，但底面已经弯曲到了三维，高实际上在第四维。

• 如果被积函数为 1，则各种积分均表示被积区域的大小
  一元积分表示线段长度；
  二重积分表示积分区域的面积；
  三重积分表示积分区域的体积；
  第一类曲线积分表示积分曲线的长度；
  第一类曲面积分表示积分曲面的面积。

物理意义

一元积分表示杆的质量；
二重积分表示薄片的质量；
三重积分表示物体的质量；
第一类曲线积分表示弯曲杆的质量；
第一类曲面积分表示弯曲薄片的质量；
第二类曲线积分表示变力做功；
第二类曲面积分表示通量。