f(x) = xlnx 曲线赏析

一、$y=x^a\ln x（a>0）$

图像

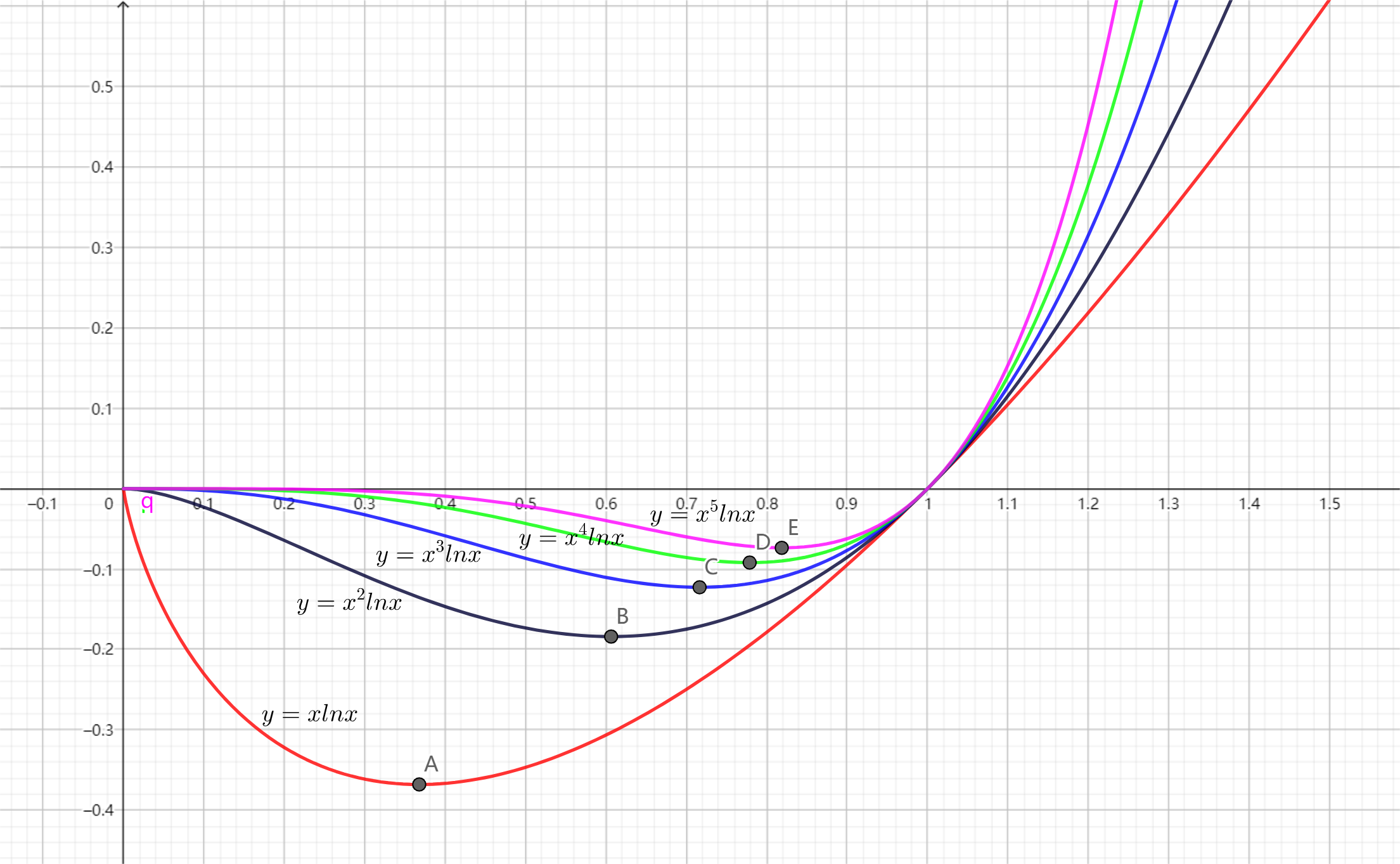
曲线从下至上的解析式

• 红：$y=x\ln x$
• 黑：$y=x^2\ln x$
• 蓝：$y=x^3\ln x$
• 绿：$y=x^4\ln x$
• 橙：$y=x^5\ln x$

极值点

$x=e^{-1/a}$

极限

$\lim_{x\to0^+}x^a\ln x=0（a>0）$

二、$y=x(\ln x)^b（b>0）$

图像

• $b$ 为偶数
  
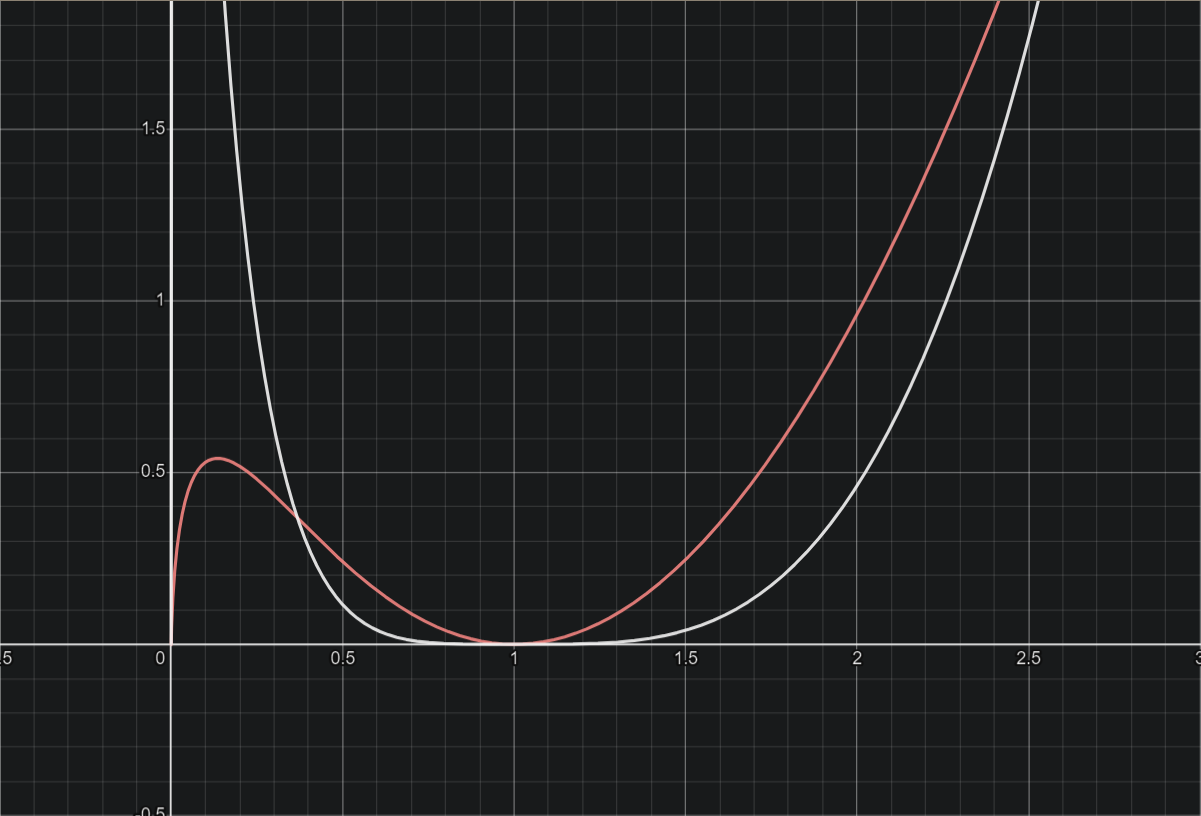
• $b$ 为奇数
  

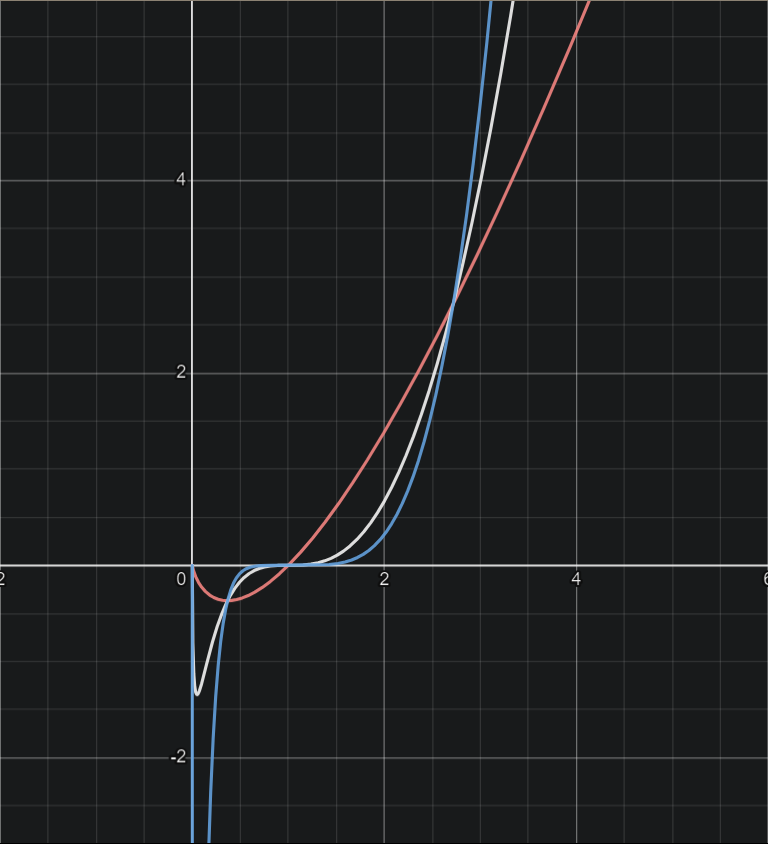
参数特性

随着 $b$ 不断递增，函数的极值点不断减小，极值不断增大

极限

$\lim_{x\to0^+}x(\ln x)^b=0$

三、总结

$\lim_{x\to0^+}x^a(\ln x)^b=0（a>0）$