外摆线赏析
发表于|更新于|高数
形成过程
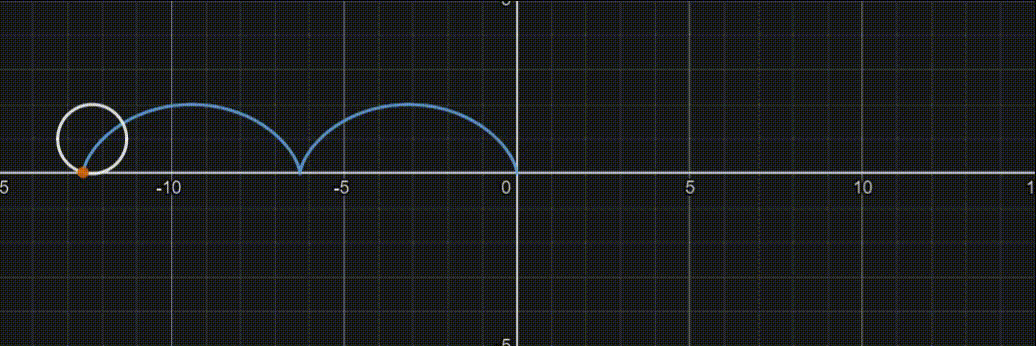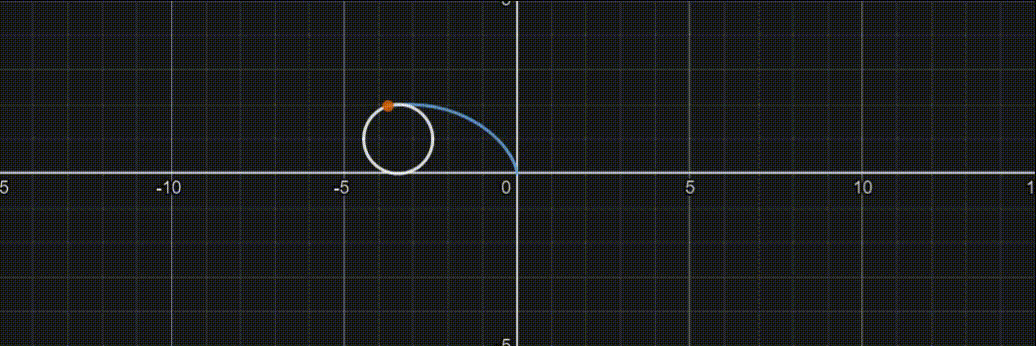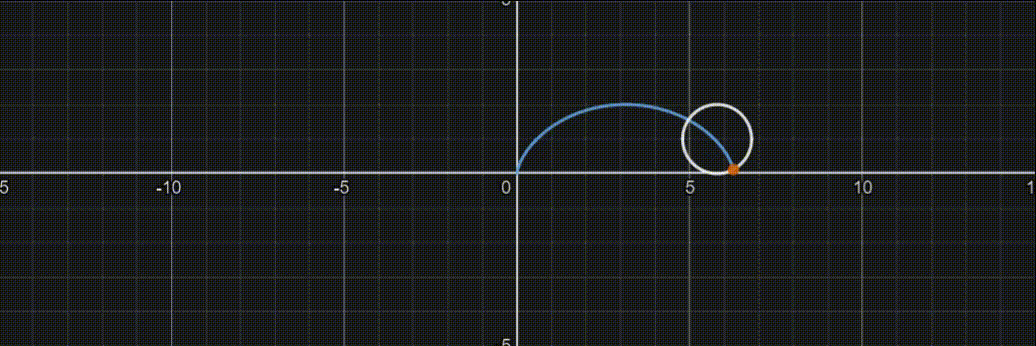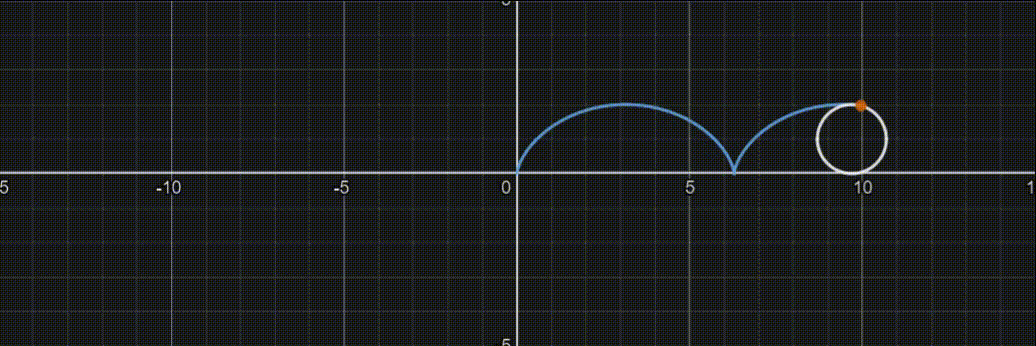
参数方程
{x=a(t−sint)y=a(1−cost)(2kπ<t<2(k+1)π),k=0,±1,±2,…)
分析
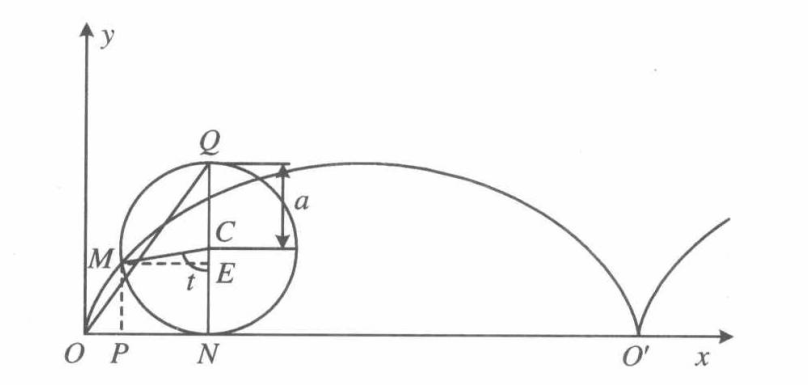

导数
dxdy=cot2t
dx2d2y=2a(1−cost)−csc22t
摆线图像
-
a>0
dx2d2y<0 则曲线为凸函数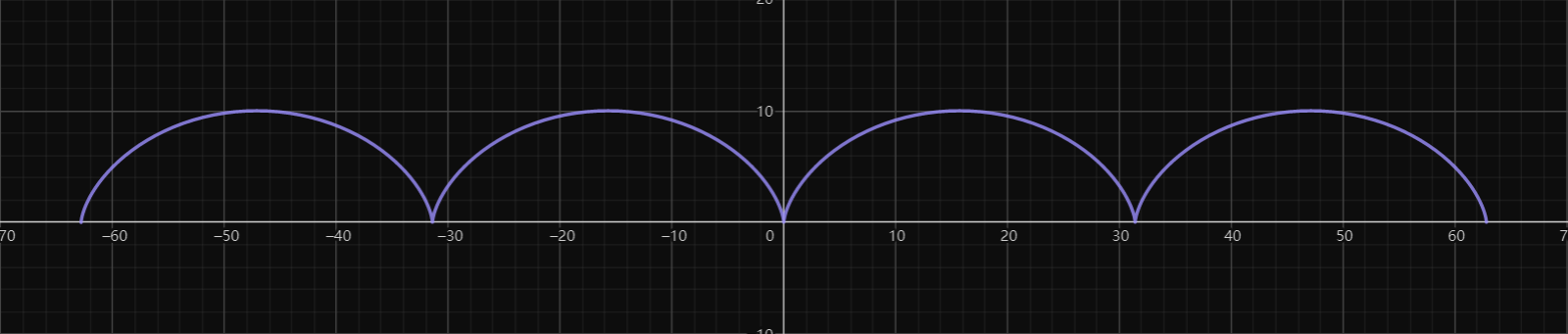
-
a<0
dx2d2y>0 则曲线为凸函数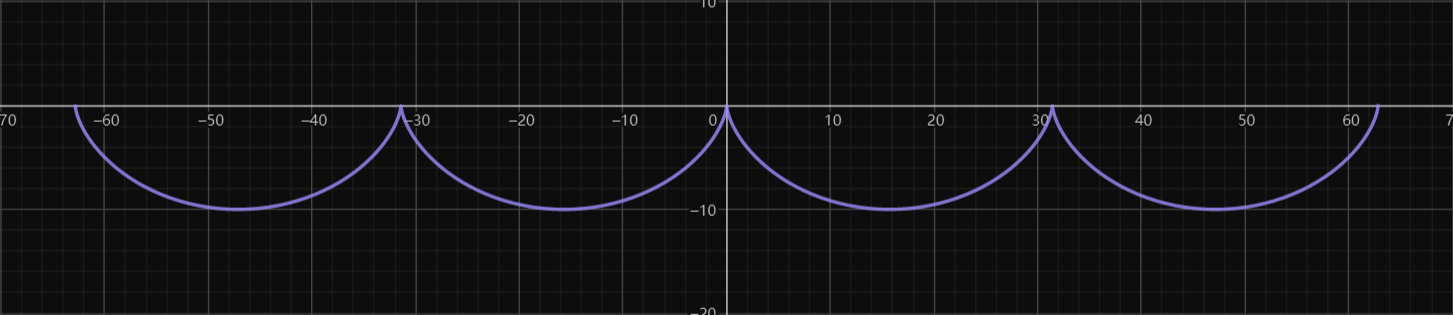
文章作者: 邹惟一
版权声明: 本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 ZouWeiyi's Home!
