高数小知识点

1、
$\dfrac{|x|}{x^2} = \dfrac{|x|}{|x|^2} = \dfrac{1}{|x|}$
$|x|^a=|x^a|$
$x$ 的符号：$\dfrac{x}{|x|}$ 或 $\dfrac{|x|}{x}$
$(\dfrac{1}{|x|})'=-\dfrac{|x|}{x^3}=-\dfrac{|x|}{x|x|^2}=-\dfrac{1}{x|x|}$

2、
一阶可导：函数可以求一阶导数，但求出的导数可能连续也可能不连续
一阶连续导数：函数可以求一阶导数，且导数连续
连续递增：函数连续并且递增

3、$f(x)\in D^2(a, b)$​ 表示 $f(x)$​ 在 $(a, b)$​ 二阶可导

4、无穷大 $\pm$ 有界量 = 无穷大

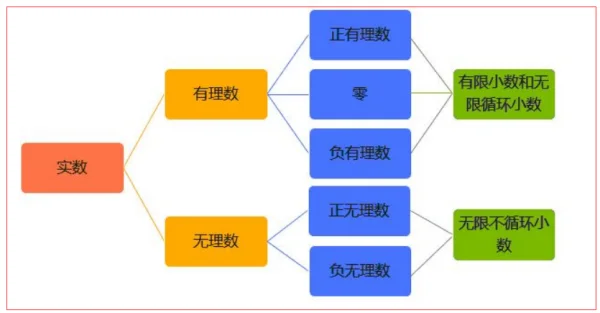
5、
常数：固定不变的数值。如圆的周长和直径的比 π
有理数：整数（正整数、0、负整数）和分数的统称
无理数：也称为无限不循环小数，不能写作两整数之比。如圆的周长和直径的比 π，欧拉数 e，黄金比例 φ

6、实系数多项式因式分解定理：每个次数不小于1的实系数多项式在实数域上都可以唯一地分解成一次因式与二次不可约因式的乘积。

7、$[a, b]$ 暗含 $b>a$

8、$\sin^nx$ 和 $\cos^nx$ 的最小正周期
当 $n$ 为偶数：$T=\pi$
当 $n$ 为奇数：$T=2\pi$

9、绘制反三角函数图像

• 画一个坐标系
• 把纸顺时针旋转 90 度，画上原函数图像
• 把纸转回来，将图像关于 y 轴作对称

10、阶乘的运算
$2^n*n!=(2n)!!$
$\dfrac{n!}{n!!}=(n-1)!!$

11、
$2\sin^2x\cos^2x=\sin^22x$
$\int_0^{\pi/2} \sin x \ \mathrm dx=\int_0^{\pi/2} \sin2x \ \mathrm dx$

12、
$f(x)$ 可导，$|f(x)|$ 不一定可导
$|f(x)|$ 的最大值点一定是 $f(x)$ 的最值点
$|f(x)|$ 的最小值点可能是 $f(x)$ 的零点，也可能是 $f(x)$ 的最值点